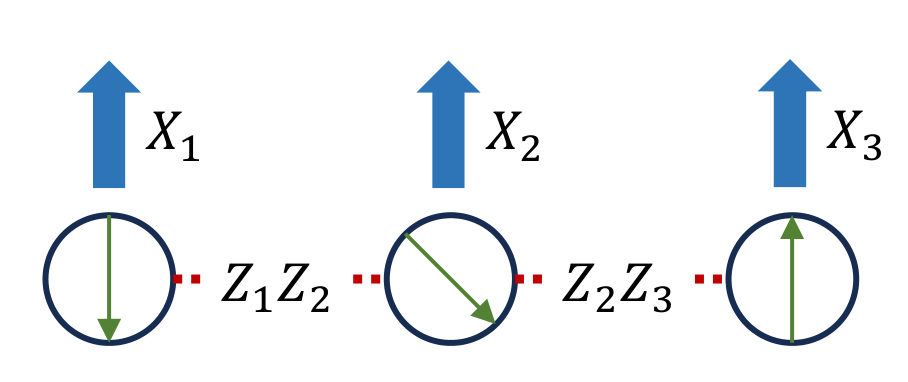Simulate Ising model on multiple devices

Published: Aug 5, 2023 by Yuxiang Peng

Here we present a case study where we program 6-site Ising models and deploy them on QuEra, IBM, and IonQ devices for a cross-platform comparison.

Programming an Ising model

We consider two Ising models with topology of chain and cycle correspondingly. Mathematically, the chain Ising model reads $H_1=\sum_{j=1}^{n-1} Z_{j}Z_{j+1}+\sum_{j=1}^n X_j$ and the cycle Ising model $H_2=H_1 + Z_1Z_{n}$, and we simulate them for $T=1$.

These systems can be programmed in SimuQ by

from simuq import QSystem, qubit
n, T = 6, 1.0
ising = QSystem()
q = [qubit(ising) for i in range(n)]
H = 0
for i in range(n - 1) :
    H += q[i].Z * q[i + 1].Z
for i in range(n) :
    H += q[i].X
if is_chain == False :
    H += q[0].Z * q[n - 1].Z
ising.add_evolution(H, T)

Deploy to multiple platforms

QuEra’s Rydberg atom arrays

QuEra currently supports global laser control and atom position configurations. We can access QuEra’s Aquila through AWS Braket, which supports at most 256 atoms.

We can deploy the cycle Ising model on Aquila one. To reduce error, we scale the Hamiltonian and evolution time by a constant factor $s=3.5$, so we evolve $H_2/s$ for $sT$ time. We can compile qs via Braket provider onto quera’s Aquila system with rydberg2d_global AAIS. The visualization by calling visualize() method of a Braket provider generates

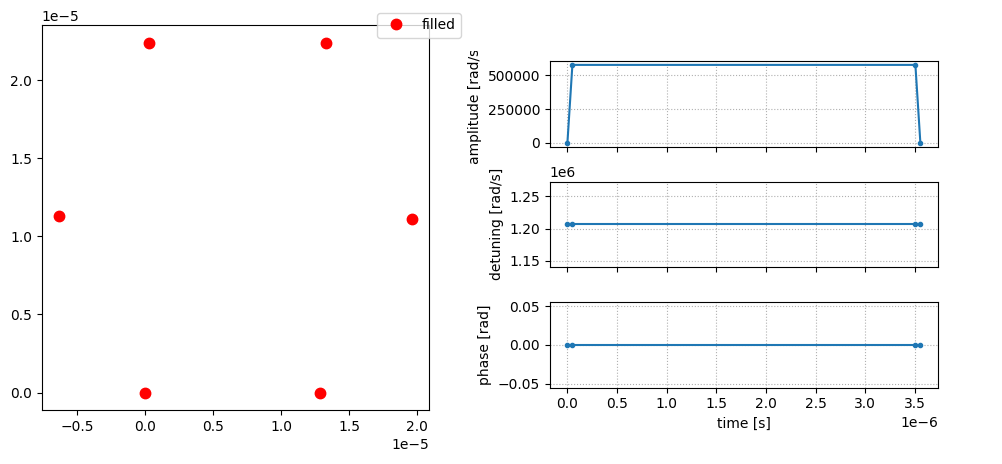
Pulse schedule of QuEra for a cycle Ising model

The chain Ising model, on the other hand, requires local laser configuration because of the different compensation of $Z_j$ terms due to different positions, hence cannot be compiled on current QuEra devices.

IonQ’s ion traps

We realize Heisenberg AAIS on IonQ devices which may compile the Ising models above. We employ IonQ’s native gates to reduce the errors, including the partially entangling Molmer Sorenson gates.

IBM’s transmon arrays

We realize Heisenberg AAIS on IBM devices with rescaled cross-resonance gates from the most updated calibration data. Due to the connectivity limitation of IBM devices, there is no 6-vertex cycle. By default we do not assume SWAP gates, so we cannot compile the 6-vertex cycle Ising model on IBM devices. The 6-vertex chain Ising model can be successfully compiled on most IBM devices.

Result analysis

We compare the measurement results at different time to the classical simulation results obtained from the QuTiP provider. Since QuEra does not support topology, we calculate the total variation distance $TV(P_1, P_2)=\frac{1}{2}\sum_x \lvert P_1[x]-P_2[x]\rvert$ where $P[x]$ is the frequency of obtaining measurement result $x$ on devices. The comparison of the error rates of different devices are presented below:

Error rates of different devices on Ising models